, 3 min read
Steve Jobs on Bicycles
Original post is here eklausmeier.goip.de/blog/2023/07-01-steve-jobs-on-bicycles.
1. Energy efficiency. Steve Jobs was impressed by the efficiency of the human riding a bike.
Steve Jobs has cited this comparison multiple times during his life. Probably he was referring to this chart in Scientific American:
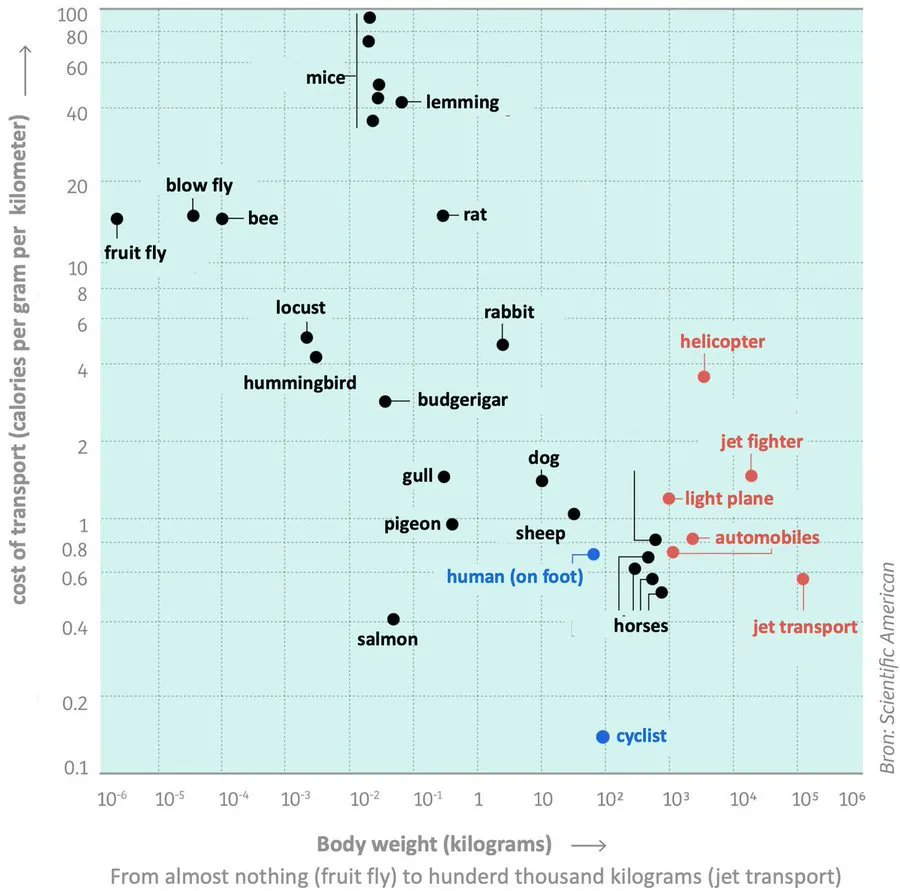
Bicycles are very efficient, see The science of bicycles by Chris Woodford.
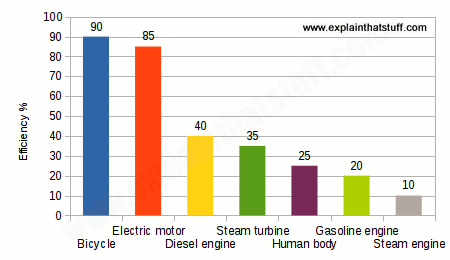
More on the efficiency is here: stackexchange: Does a human on a bicycle travel more efficiently than any other species?.
How the bicycle beats evolution and why Steve Jobs was so taken with this fact by Carlton Reid.
2. Differential equation. Below statements and figures are coped from Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review by J.P Meijaard, Jim M Papadopoulos, Andy Ruina, A.L Schwab. A local copy is here. Also see English Wikipedia Bicycle and motorcycle dynamics from where I copy the eigenvalue part.
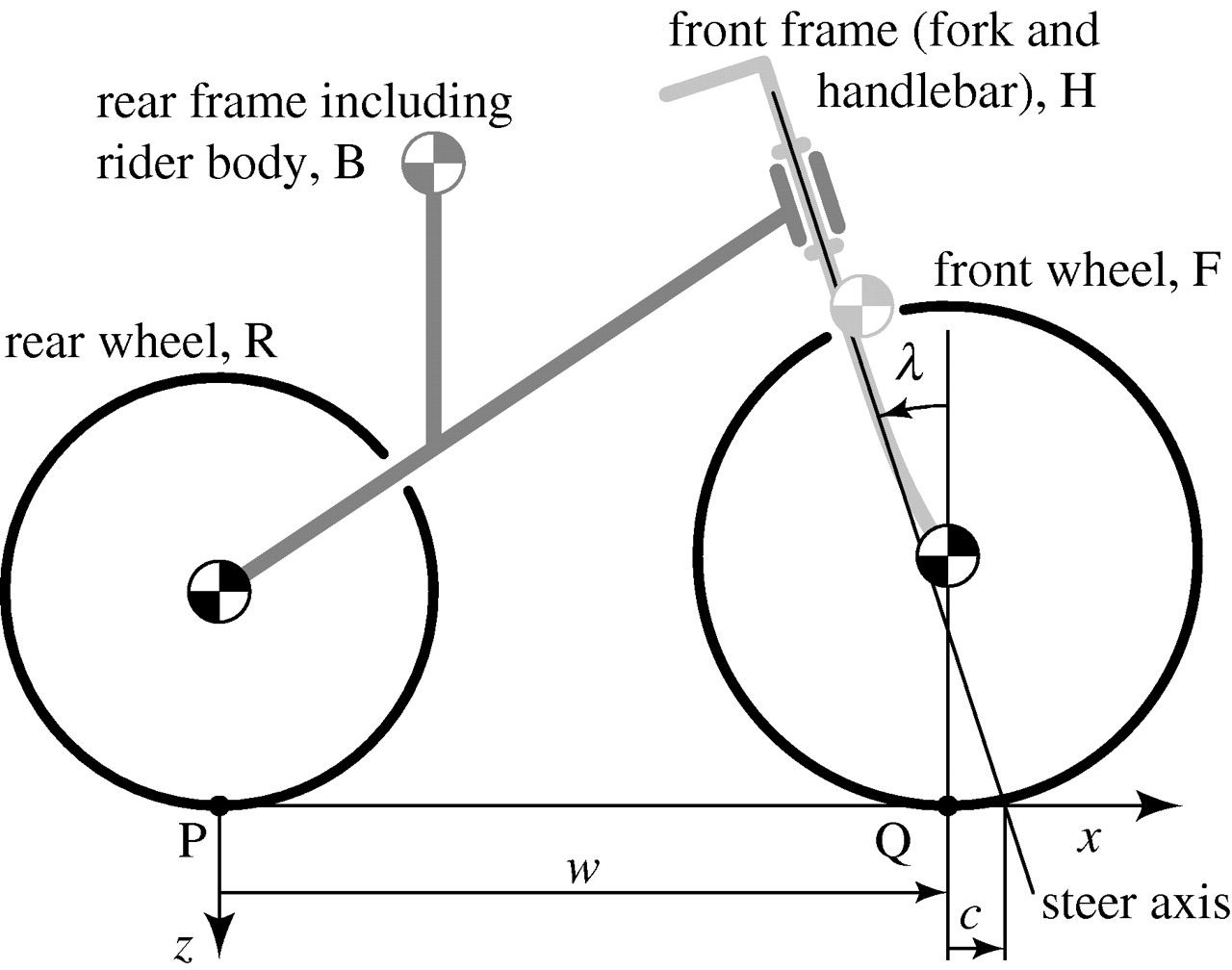
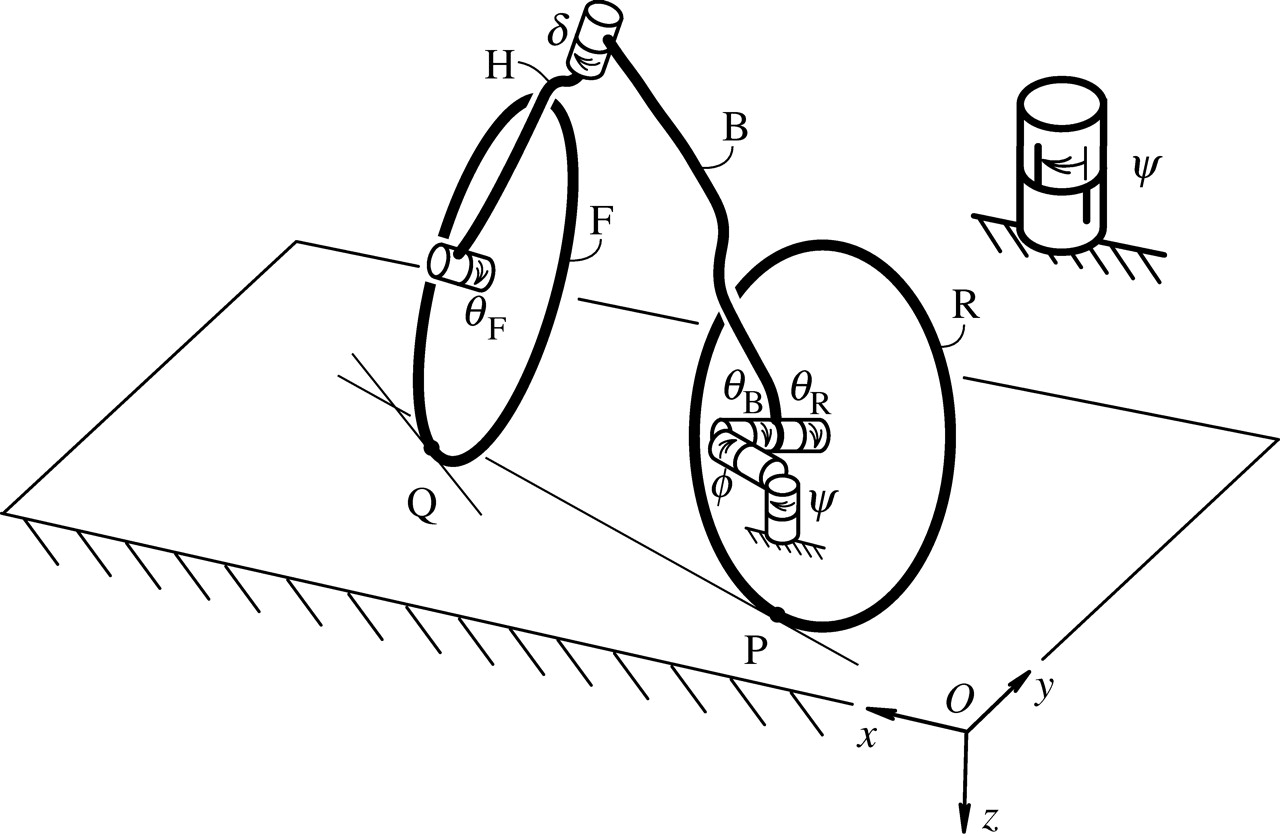
Model parameters are given in below table.
| parameter | symbol | value for benchmark |
|---|---|---|
| wheel base | w | 1.02 m |
| trail | c | 0.08 m |
| steer axis tilt ($\pi/2$−head angle) | $\lambda$ | $\pi/10 \hbox{rad} (90^\circ–72^\circ)$ |
| gravity | g | $9.81 \hbox{N} \hbox{kg}^{−1}$ |
| forward speed | v | various m s-1 |
| rear wheel R | ||
| radius | $r_R$ | 0.3 m |
| mass | $m_R$ | 2 kg |
| mass moments of interia | $\left(I_{Rxx},I_{Ryy}\right)$ | (0.0603, 0.12) kg m2 |
| rear body and frame assembly B | ||
| position center of mass | $\left(x_B,z_B\right)$ | (0.3, -0.9) m |
| mass | $m_B$ | 85 kg |
| mass miments of interia | $\begin{pmatrix}I_{Bxx}&0&I_{Bxz}\cr 0&I_{Byy}&0\cr I_{Bxz}&0&I_{Bzz}\cr\end{pmatrix}$ | $\begin{pmatrix} 9.2&0&2.4\cr 0&11&0\cr 2.4&0&2.8\cr\end{pmatrix}$ kg m2 |
| front handlebar and fork assembly H | ||
| position center of mass | $\left(x_H,z_H\right)$ | (0.9, -0.7) m |
| mass | $m_H$ | 4 kg |
| mass moments of inertia | $\begin{pmatrix}I_{Hxx}&0&I_{Hxz}\cr 0&I_{Hyy}&0\cr I_{Hxz}&0&I_{Hzz}\cr\end{pmatrix}$ | $\begin{pmatrix}0.05892&0&-0.00756\cr 0&0.06&0\cr -0.00756&0&0.078\cr\end{pmatrix}$ kg m2 |
| front wheel F | ||
| radius | $r_F$ | 0.35 m |
| mass | $m_F$ | 3 kg |
| mass moments of inertia | $\left(I_{Fxx},I_{Fyy}\right)$ | (0.1405, 0.28) kg m2 |
The dynamic can be represented by a single fourth-order linearized ordinary differential equation or two coupled second-order differential equations, i.e., in matrix form
where the time-varying quantities are $q = \left[\phi, \delta\right]^T$ and $f = \left[T_\phi, T_\delta\right]^T$. The constant entries in matrices $M, C_1, K_0$ and $K_2$ are defined in terms of the 25 design parameters.
The eigenvalues of
are now of interest. If the real parts of all eigenvalues are negative, the bike is self-stable. When the imaginary parts of any eigenvalues are non-zero, the bike exhibits oscillation. The eigenvalues are point symmetric about the origin and so any bike design with a self-stable region in forward speeds will not be self-stable going backwards at the same speed.