, 2 min read
Hashing Just Random Numbers
Original post is here eklausmeier.goip.de/blog/2013/06-30-hashing-just-numbers.
My recent project had some issues with hashing some 10 million numbers. To analyze the matter I wrote a small test program, see numberhash.c.
I wanted to know which influence the following factors play:
- hashing just numbers (no alphabetic characters)
- ASCII vs. EBCIDC
- choice of hash function
- load factor
- distribution of collisions
The results for random numbers so far go like this:
- hash function is of lesser importance
- load factor is important
- character set is not important
The little program numberhash.c can test four different hash functions (-f), can vary the size of the hash (-h), and the length of the string of digits (-l). Collision resolution is by linear probing. Linear probing was used as the original hashing algorithm was coded in COBOL, where linked lists are not that common. Random numbers are generated by random() seeded by /dev/urandom.
Compile numberhash.c with
cc -O3 -Wall -Wno-pointer-sign numberhash.c -o numberhash -lcrypto
The following hash functions are implemented:
- Kernighan & Ritchie: h = 31 * h + key[i]
- SHA1
- just take the digit string and then calculate modulo hashsize
- h = 2 * h + key[i] * key[i]
Here is an example output for 1 million random numbers, each having default length of 10 digits:
$ time ./numberhash -f0 -n1000001 -h1400093
Number of random numbers: 1000001, hash size = 1400093
Total number of collisions: 1249237 = 124.923575%, load factor: 71.423898
0 400130 28.58
1 417348 29.81
2 267712 19.12
3 148032 10.57
4 79356 5.67
5 41479 2.96
6 21747 1.55
7 11471 0.82
8 6067 0.43
9 3222 0.23
10 1645 0.12
11 874 0.06
12 478 0.03
13 270 0.02
14 149 0.01
15 54 0.00
16 25 0.00
17 23 0.00
18 7 0.00
19 3 0.00
20 1 0.00
21 0 0.00
22 0 0.00
23 0 0.00
24 0 0.00
25 0 0.00
26 0 0.00
27 0 0.00
28 0 0.00
29 0 0.00
real 0m0.296s
user 0m0.224s
sys 0m0.068s
Changing the load factor to above 99% reduces waste, but multiplies the running time by factor of 30.
$ time ./numberhash -f0 -n1000001 -h1001093
Number of random numbers: 1000001, hash size = 1001093
Total number of collisions: 260986225 = 26098.596401%, load factor: 99.890919
0 1137 0.11
1 1921 0.19
2 2183 0.22
3 2064 0.21
4 2055 0.21
5 1987 0.20
6 2008 0.20
7 2008 0.20
8 1996 0.20
9 2019 0.20
10 1985 0.20
11 2164 0.22
12 2176 0.22
13 2179 0.22
14 2097 0.21
15 2246 0.22
16 2276 0.23
17 2351 0.23
18 2312 0.23
19 2307 0.23
20 2433 0.24
21 2472 0.25
22 2664 0.27
23 2506 0.25
24 2505 0.25
25 2378 0.24
26 2473 0.25
27 2433 0.24
28 2409 0.24
>29 937349 93.63
real 0m6.244s
user 0m6.196s
sys 0m0.044s
And here are the results for a load factor of 95%.
$ time ./numberhash -f0 -n1000001 -h1053991
Number of random numbers: 1000001, hash size = 1053991
Total number of collisions: 9398528 = 939.851860%, load factor: 94.877565
0 54031 5.13
1 85178 8.08
2 88536 8.40
3 81647 7.75
4 73594 6.98
5 66787 6.34
6 60495 5.74
7 54382 5.16
8 48231 4.58
9 43684 4.14
10 38778 3.68
11 34399 3.26
12 30569 2.90
13 27584 2.62
14 25040 2.38
15 22961 2.18
16 20714 1.97
17 18643 1.77
18 17117 1.62
19 15577 1.48
20 13834 1.31
21 12723 1.21
22 11651 1.11
23 10546 1.00
24 9839 0.93
25 8697 0.83
26 7726 0.73
27 6962 0.66
28 6404 0.61
>29 57662 5.47
real 0m0.439s
user 0m0.392s
sys 0m0.044s
First and last run are as below:
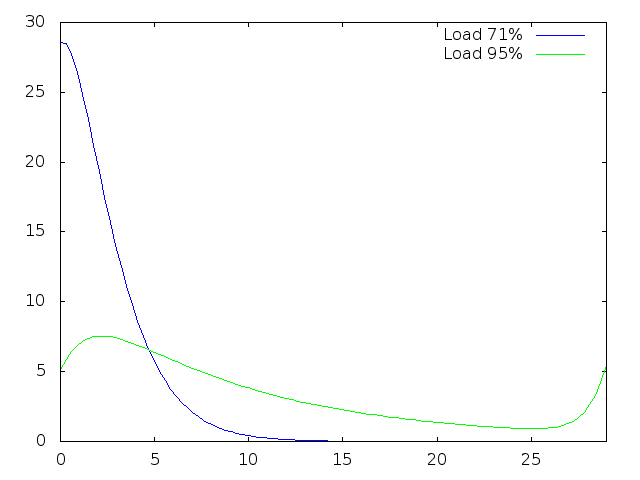
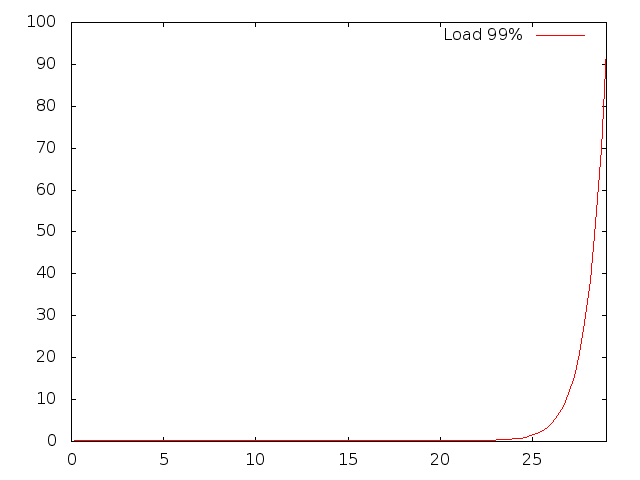
"Catastrophic" run is:
gnuplot's with
set terminal png
set output 'load7195.png'
plot [0:29] 'numberh.txt' index 0 using 1:3 smooth bezier lt rgb "blue" title "Load 71%", 'numberh.txt' index 2 using 1:3 smooth bezier lt rgb "green" title "Load 95%"
set output 'load99.png'
plot [0:29] 'numberh.txt' index 1 using 1:3 smooth bezier lt rgb "red" title "Load 99%"