, 5 min read
CPU Usage Time Is Dependant on Load
Original post is here eklausmeier.goip.de/blog/2012/12-29-cpu-usage-time-dependant-on-load.
I wanted to write a short benchmark for my son to demonstrate that the AMD Bulldozer 8 core CPU is better than a 6 core CPU from AMD when computing with integers. So I wrote a short C program to compute a recurrence relation using integers only, see C code below. When I ran this program on one core, then two cores, then three cores, and so on, I was a little bit surprised to see that the CPU usage time grew. Indeed, it grew quite significantly: from 20 to 60% up! Once all cores of the CPU are used then the CPU usage does no longer increase. In this case it does seem to have reached its equilibrium.
The AMD CPU is a FX 8120, 3.1GHz. For comparison I used an Intel i7-2640, 2.8GHz, 4 core CPU.
I compiled
cc -Wall -O3 intpoly.c -o intpoly
and then ran the program as follows
for i in `seq 1 24`; do echo 2 -1 0 -2 | time -f "%e %U %S" ./intpoly -f -n0 & done
I varied the number of runs from 1 to 24, as indicated in the line above.
The average CPU usage results were as follows on an 8 core AMD Bulldozer:
runs AMD i7 AMD/fp
1 2.44 2.14 5.86
2 2.48 2.25 6.02
3 2.84 2.85 6.84
4 2.96 4.28 6.91
5 3.00 4.34 7.00
6 3.44 4.35 7.12
7 3.82 4.35 7.22
8 4.10 4.34 7.30
9 4.11 4.35 7.28
10 4.11 4.36 7.28
16 4.11 4.38 7.30
24 4.11 4.38 7.31
64 4.12 4.39 7.30
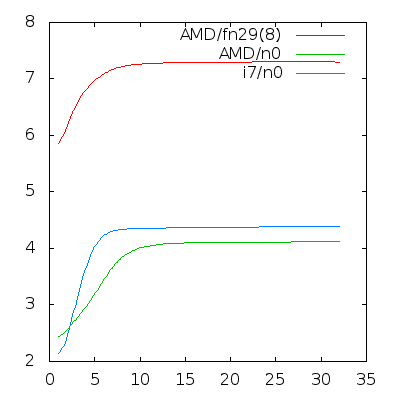
The times given above are not the elapsed time! Of course, elapsed time can be calculated according
number of runs / number of cores * equilibrium time
For example, the AMD used 33 seconds of elapsed time for 64 tasks, while the i7 used 69 seconds, so more than two times as long.
So, I got my result, stating that the more cores you have in your CPU the smaller the elapsed time will be. What I did not expect was, that in the range from 1 to the number of cores in the CPU, usage and elapsed time increase. So some distribution of work must be going on within the CPU, or some kind of contention. If somebody knows why, please leave a note. This behaviour is independent from AMD or Intel, and independent whether one uses integer calculation or double precision.
The C program, named intpoly, reads some initial values from stdin. With -f switch it computes all values in double precision, without -f it uses integer arithmetic. Switch -n tells how many iterations, -m the number of rounds.
/* Evaluate difference scheme.
It has generating polynomial
4 2
x - 2 x + 1
and has real roots:
2 2
(x - 1) (x + 1)
So all values should remain bounded.
Floating point case: Polynomial is
3 2
4 25 x 311 x 29 x 14
x - ----- - ------ + ---- + --
72 216 108 27
with roots
8 2 7
(x - 1) (x - -) (x + -) (x + -)
9 3 8
Elmar Klausmeier, 29-Dec-2012
*/
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <limits.h>
int main (int argc, char *argv[]) {
register int i, x[5];
int c, i0=0, m=1, xin[5], fp=0, prtflag = 0;
double xd[5];
while ((c = getopt(argc,argv,"fm:n:p")) != -1) {
switch (c) {
case 'f':
fp = 1;
break;
case 'm':
m = atoi(optarg);
break;
case 'n':
i0 = atoi(optarg);
break;
case 'p':
prtflag = 1;
break;
default:
printf("%s: unknown flag %c\n",argv[0],c);
return 1;
}
}
if (i0 == 0) i0 = INT_MAX;
if (m == 0) m = 1;
if (fp) goto fp_section;
// Integer computation
if ((c = scanf("%d %d %d %d", &xin[0],&xin[1],&xin[2],&xin[3])) != 4) {
printf("%s: Need exactly 4 input arguments via stdin, read only %d\n",argv[0],c);
return 3;
}
x[0] = xin[0];
x[1] = xin[1];
x[2] = xin[2];
x[3] = xin[3];
//x[4] = xin[4];
while (m-- > 0) {
i = i0;
while (i-- > 0) {
x[4] = 2*x[2] - x[0];
#ifdef PRTFLAG
//x[4] = (75*x[3] + 311*x[2] - 58*x[1] - 112*x[0]) / 216;
if (prtflag || x[4] > 9999999999 || x[4] < -9999999999)
printf("%d\n",x[4]);
#endif
x[0] = x[1];
x[1] = x[2];
x[2] = x[3];
x[3] = x[4];
//x[4] = x[5];
}
}
printf("%d\n",x[4]);
return 0;
fp_section:
// Floating-point computation
if ((c = scanf("%lf %lf %lf %lf %lf", &xd[0],&xd[1],&xd[2],&xd[3],&xd[4])) != 4) {
printf("%s: Need exactly 4 input arguments via stdin, read only %d\n",argv[0],c);
return 3;
}
while (m-- > 0) {
i = i0;
while (i-- > 0) {
xd[4] = 25.0/72*xd[3] + 311.0/216*xd[2] - 29.0/108*xd[1] - 14.0/27*xd[0];
#ifdef PRTFLAG
if (prtflag || xd[4] > 9999999999 || xd[4] < -9999999999)
printf("%f\n",xd[4]);
#endif
xd[0] = xd[1];
xd[1] = xd[2];
xd[2] = xd[3];
xd[3] = xd[4];
}
}
printf("%f\n",xd[4]);
return 0;
}
A version of this program can also be found on GitHub in intpoly.c.
1. Comment. By brucedawson | April 21, 2013 at 18:19.
You say “the more cores you have in your CPU the smaller the elapsed time will be. What I did not expect was, that in the range from 1 to the number of cores in the CPU, usage and elapsed time increase.” — isn’t that contradicting yourself, since elapsed time can’t both get smaller and increase?
Also, as my counting-to-ten post that you linked to says, you can’t trust the CPU usage information from ‘time’. You should use a separate program to monitor total system CPU usage, in a more reliable way. If you redo your tests with that (and label your graph and table axes!) then maybe it will all make sense.
2. Comment. eklausmeier | April 21, 2013 at 21:34 Edit
Thank you for your post. It is indeed not easy to get the point. Assume the time command is correct in reporting elapsed time, which you also state in your article. Even if you do not trust the time command, when you do something like (date;command;date) it will give you similar results.
Now assume a fixed number of jobs for our artificial problem at hand, say 64. The statement is: The more cores you have, the quicker you can solve the problem. Every job can run independently. A machine with two cores will take longer (elapsed time over all processes) than a machine with eight cores, all else being equal. First I just wanted to prove just that, which I did.
The problem I observed now is, that you cannot just divide the number of jobs by your number of cores. The relation is apparently not linear, see the graph. What is puzzling, even when you have enough free cores available on your machine, elapsed time per job increases in the range one to number of cores in your CPU, 8 in my case. In the Phoronix forum (Thread: Slowdown when computing in parallel on multicore CPU) I got a reply which explained this phenomen with CPU migration. This seems to be a deficiency/bug in releases before kernel version 3.8.