, 2 min read
Fast unary decoding
Computers store numbers in binary form using a fixed number of bits. For example, Java will store integers using 32 bits (when using the int type). This can be wasteful when you expect most integers to be small. For example, maybe most of your integers are smaller than 8. In such a case, a unary encoding can be preferable. In one form of unary encoding, to store the integer x, we first write x zeroes followed by the integer 1. The following table illustrates the idea:
| Number | 8-bit binary | unary |
|---|---|---|
| 0 | 00000000 | 1 |
| 1 | 00000001 | 01 |
| 2 | 00000010 | 001 |
Thus, to code the sequence 0, 0, 1, 2, 0, we might use 1-1-01-001-1 stored as the byte value 11010011. To recover the sequence from a unary coded stream, it suffices to seek the bits with value 1. A naive decoder will simply examine each bit value, in sequence. (See code sample.) We should not expect this approach to be fast.
A common optimization is to use a table look-up. Indeed, we can construct a table with 256 entries where, for each byte value, we store the number of 1s and their position. (See code sample.) This can be several times faster.
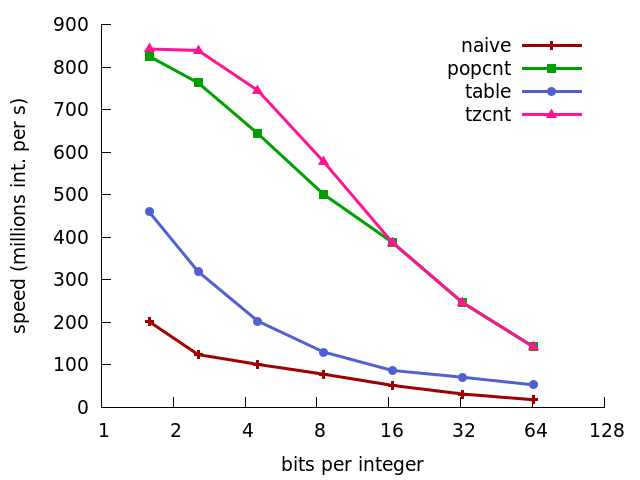
A possibly faster alternative is to use the fact that all modern processors have Hamming weight instructions: fast instructions telling you how many bits with value 1 are present in a 64-bit word (popcnt on Intel processors supporting SSE4.2). Similarly, one can use an instruction that counts the number of trailing zeroes (lzcnt or bsf on Intel processors). We can put such instructions to good use for unary decoding. (See popcnt code sample and See lzcnt/bsf code sample.)
According to my tests, on recent Intel processors, the latter approach is much faster, decoding integers at speeds of over 800 millions integers per second, being roughly twice as fast as a table-based approach. See the next figure.
As usual, my source code is freely available.