18th August 2009, 3 min read

Do hash tables work in constant time?

Theory in Computer Science—as in any other field—is based on models. These models make many hidden assumptions. This is one of the fundamental reason why pure theory is wasteful. We must constantly revisit our old assumptions and run experiments to determine whether our models are useful.

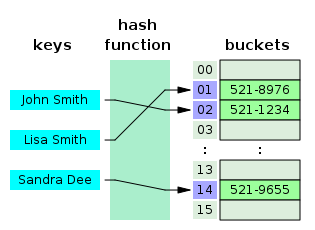
Hash tables are a fundamental data structure. They are part of every elementary introduction to Computer Science. From a programmer’s point of view, they associate keys with values. Hash tables go back to the beginnings of Computer Science even though new variations keep being invented (e.g., Cuckoo hashing). Incredibly, hash tables were just recently integrated in the C++ language, but less conservative languages like Java, Python, Ruby, Perl, PHP, all have hash tables built-in.

The secret sauce is that the key is first transformed (or hashed) to a number between 1 and m corresponding to a cell in an array. As long as this number of generated with sufficient randomness, hash tables are almost equivalent to looking up values in an array—except for the overhead of hashing the key.

Thus, everyone knows that hash table queries run in amortized constant time. That is, as the number of keys increases, the average time necessary to recover a key-value pair does not increase.

But wait! How do we compute hash values? Consider the standard universal hashing technique described in Corman et al. Introduction to Algorithms. We pick any prime number m. Pick randomly a number a in [0,m). Then h(x)= x a modulo m is a universal hash function. Multiplications of numbers in [0,m) can almost be done in time O(log m).  For the purposes of hash tables, the number m must be close to the number of different keys n. Thus—formally—hash tables often run in time O(log n). Am I being pedantic? Does the time required to multiply integers on modern machine depend on the size of the integers? It certainly does if you are using vectorization_. And vectorization is used in commercial databases! And what if your key is a string? As you have more keys, you are more likely to encounter longer strings which take longer to hash.